Statistical indicators
國內外統計指標簡介
#R square
根據多數相關文獻,為了評估並比較各國不同之規範的收縮預測結果,多使用確定係數作為一公平、客觀的指標。其定義如下所示:
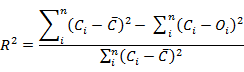
其中:
n = 資料點總數
當
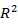 愈靠近1 時,表示預測結果相當準確,而當
愈靠近1 時,表示預測結果相當準確,而當
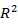 愈趨近0時,表示預測結果不佳。
愈趨近0時,表示預測結果不佳。
#Bazant and Baweja
此統計指標由Bažant提出,主要特色為針對潛變、收縮的量測特性進行改善,
將每個實驗時間點依對數時間區間分割成0至9.9天、10至99.9天、100至1000天等以此類推,並將每個資料點賦予一權重
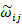 。
由於收縮實驗之量測習慣多為前期頻繁地量測,後期則大量減少量測頻率。
此類似對數時間的量測方式造成前期與後期資料點數量相差甚大,因此,透過計算
。
由於收縮實驗之量測習慣多為前期頻繁地量測,後期則大量減少量測頻率。
此類似對數時間的量測方式造成前期與後期資料點數量相差甚大,因此,透過計算
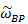 (經過權重調整後的資料點之變異係數)可以針對不同資料點數量的時間區間賦予權重,
當
(經過權重調整後的資料點之變異係數)可以針對不同資料點數量的時間區間賦予權重,
當
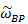 愈接近0%時,預測值與觀測值為完全相關。公式定義如下所示:
愈接近0%時,預測值與觀測值為完全相關。公式定義如下所示:
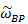 =
=
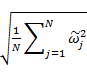
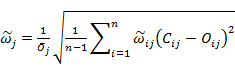
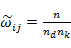
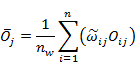
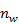 = 一個資料組中所有資料點之權重總合
= 一個資料組中所有資料點之權重總合
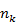 = 在對數時間區間k中的資料點數
= 在對數時間區間k中的資料點數
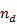 = 一個資料組中之對數時間區間數
= 一個資料組中之對數時間區間數
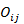 = 在第j個資料組中的第i個資料點之觀測值
= 在第j個資料組中的第i個資料點之觀測值
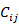 = 在第j個資料組中的第i個資料點之預測值
= 在第j個資料組中的第i個資料點之預測值
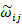 = 在第j個資料組中的第i個資料點之權重
= 在第j個資料組中的第i個資料點之權重
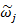 = 第j個資料組之變異係數
= 第j個資料組之變異係數
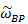 = 整體之變異係數
= 整體之變異係數
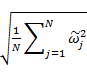
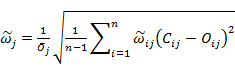
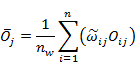
其中:
n = 在第j個資料組中之資料點數
N = 資料組數
此統計指標可看出試驗值與預測值經權重後的偏差程度,突顯中、長期對於整筆資料的重要性,較符合用於混凝土之收縮預測,但由於最後結果為各區間權重後之變異係數平方相加再開根號,雖經權重修正,但仍可能被殘差相對較大之少數資料組控制。
#CEB statistical indicators
此統計指標由Müller&Hilsdorf
所提出,將實驗時間點分割成0至10天、11至100天、101至365天、366至730天、731至1095天、與1095天以上等六個資料組區間。此統計有以下三個指標:
變異係數
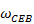 為:
為:
其中:
n = 資料組數
變異係數
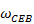 主要作用為評估預測值與觀測值間之偏差量,當其等於0%時,預測值與觀測值為完全相關。
主要作用為評估預測值與觀測值間之偏差量,當其等於0%時,預測值與觀測值為完全相關。
此變異數有幾個問題,其一為當第i個資料組中只有少數的資料點數時,對變異數會產生顯著的影響;反之,如果資料點數很多時,對變異數的影響幅度則會下降,
其結果導致資料點數相對較少的資料組會影響整體的變異數。
其二為當資料點數過於集中在前期而後期點數稀少時,會造成前期的
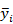 很小而給予其很大的權重
很小而給予其很大的權重
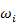 ,造成整體的變異會由前期的資料點數影響而忽略了後期的重要性,但是對於收縮和潛變的數據分析中,其終值才是最為重要的。
,造成整體的變異會由前期的資料點數影響而忽略了後期的重要性,但是對於收縮和潛變的數據分析中,其終值才是最為重要的。
均方誤差
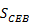 為:
為:
其中:
n = 資料組數
均方誤差
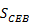 主要作用為評估預測值與觀測值之誤差佔觀測值之比例大小。當其等於0%時,預測值與觀測值為完全相關。
主要作用為評估預測值與觀測值之誤差佔觀測值之比例大小。當其等於0%時,預測值與觀測值為完全相關。
然而,權重
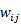 會受到
會受到
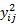 而有顯著的影響,例如在微小的收縮變異下會導致其被過度強調,而有較大的收縮變異時則會被低估,同樣導致短時間的收縮潛變會決定整體的分析而非最為重要的終值。
而有顯著的影響,例如在微小的收縮變異下會導致其被過度強調,而有較大的收縮變異時則會被低估,同樣導致短時間的收縮潛變會決定整體的分析而非最為重要的終值。
平均差
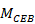 為:
為:
其中:
n = 資料組數
平均差
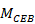 主要作用為評估所有資料點預測值為高估或低估之趨勢。當其等於1.0時,預測值與觀測值為完全相關。
主要作用為評估所有資料點預測值為高估或低估之趨勢。當其等於1.0時,預測值與觀測值為完全相關。
此平均差僅能看出預測值之整體趨勢為低估或者高估,無法得知資料點發散程度或著分布情形。
#Gardner
其將所有實驗時間點分割成3至9.9天、10至31.5天、31.6至99天、100至315天、316至999天、1000至3159天、與3160天以上等七個資料組區間。
透過計算各資料組的方均根,並除以組數求得方均根的平均,再除以觀測值的平均即可得
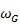 。當
。當
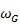 =0%時,預測值與觀測值為完全相關。公式與定義如下:
=0%時,預測值與觀測值為完全相關。公式與定義如下:
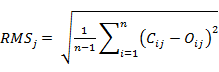
其中:
n = 一個資料組中之資料點數
N = 資料組數
可看出試驗值與預測值的偏差程度,且係將各資料組之方均根與平均先進行平均後相除,不使用變異係數平方合開根號的方式,較無受少數相對誤差較大資料組影響的問題。
